POTENCIA
La potenciación es una multiplicacion de varios factores iguales, al igual que la multiplicacion es una suma de varios sumandos iguales, (la potenciación se considera una multiplicación abreviada).
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente,
que se escribe en forma de superíndice. El exponente determina la
cantidad de veces que la base se multiplica por sí misma. Por ejemplo:

en general:

Una de las definiciones de la potenciación, por recursión, es la siguiente:
x1 = x
Si en la segunda expresión se toma a=1, se tiene que x¹ = x·x0. Al dividir los dos términos de la igualdad por x (que se puede hacer siempre que x sea distinto de 0), queda que x0=1.
Así que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacio o simplemente por analogía con el resto de números.
Para convertir una base con exponente negativo a positivo se pone la
inversa de la base, es decir que la potencia pasa con exponente
positivo.
Normalmente, las potencias con base 10, por la cantidad que
represente el exponente,esa será la cantidad de ceros en el resultado.
El resto de la bases, para sacar el resultado el número se multiplica
por sí mismo cuantas veces indique el exponente.
Propiedades de la potenciación
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
 si se cumple que
si se cumple que 
00 es una indeterminación. Que puede relacionarse con la indeterminación dado que
dado que

Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
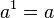
ejemplo:

Producto de potencias de igual base
El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes.

ejemplos:

División de potencias de igual base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos..
Se coloca la misma base y se restan los exponentes.

Potencia de un producto
la potencia de un producto de base (a·b) y de exponente "n" es igual
a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica
por el exponente.
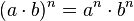
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a
elevada a la multiplicación de ambos exponentes. Se coloca la misma
base y se multiplican los exponentes. así se obtiene esta potencia
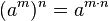
Producto de potencias de base distinta
En forma más general, la suma de dos radicaciones de base distinta a, b se puede expresar de la siguiente manera:

De tal forma que si a = b se regresa a la expresión para bases iguales.
Propiedad distributiva
a multiplicación y a
la división, pero no lo es con respecto a la suma ni a la resta.
Es distributiva con respecto a la multiplicación y división:
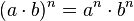

No es distributiva con respecto a la adición y sustracción:

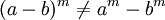
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación,
exceptuando aquellos casos en que base y exponente tienen el mismo
valor o son equivalentes.
En general:

Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.

Potencia de base 10
Toda potencia de base 10 y exponente natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
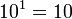

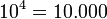

Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción no es irreductible, y en la que se cumple que
Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Potencia de números complejos
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente,
que se escribe en forma de superíndice. El exponente determina la
cantidad de veces que la base se multiplica por sí misma. Por ejemplo:

en general:

Una de las definiciones de la potenciación, por recursión, es la siguiente:
x1 = x

Si en la segunda expresión se toma a=1, se tiene que x¹ = x·x0. Al dividir los dos términos de la igualdad por x (que se puede hacer siempre que x sea distinto de 0), queda que x0=1.
Así que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacio o simplemente por analogía con el resto de números.
Para convertir una base con exponente negativo a positivo se pone la
inversa de la base, es decir que la potencia pasa con exponente
positivo.
Normalmente, las potencias con base 10, por la cantidad que
represente el exponente,esa será la cantidad de ceros en el resultado.
El resto de la bases, para sacar el resultado el número se multiplica
por sí mismo cuantas veces indique el exponente.
Propiedades de la potenciación
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
 si se cumple que
si se cumple que 
00 es una indeterminación. Que puede relacionarse con la indeterminación
 dado que
dado que
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
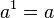
ejemplo:

Producto de potencias de igual base
El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes.

ejemplos:

División de potencias de igual base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos..
Se coloca la misma base y se restan los exponentes.

Potencia de un producto
la potencia de un producto de base (a·b) y de exponente "n" es igual
a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica
por el exponente.
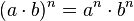
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a
elevada a la multiplicación de ambos exponentes. Se coloca la misma
base y se multiplican los exponentes. así se obtiene esta potencia
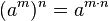
Producto de potencias de base distinta
En forma más general, la suma de dos radicaciones de base distinta a, b se puede expresar de la siguiente manera:

De tal forma que si a = b se regresa a la expresión para bases iguales.
Propiedad distributiva
a multiplicación y a
la división, pero no lo es con respecto a la suma ni a la resta.
Es distributiva con respecto a la multiplicación y división:
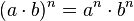

No es distributiva con respecto a la adición y sustracción:

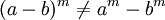
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación,
exceptuando aquellos casos en que base y exponente tienen el mismo
valor o son equivalentes.
En general:

Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.

Potencia de base 10
Toda potencia de base 10 y exponente natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
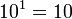

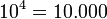

Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción no es irreductible, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Potencia de números complejos
Para cualquiera de los numeros reales  se tiene la identidad:
se tiene la identidad:
 se tiene la identidad:
se tiene la identidad:




No hay comentarios:
Publicar un comentario