martes, 8 de septiembre de 2009
POTENCIA
La potenciación es una multiplicacion de varios factores iguales, al igual que la multiplicacion es una suma de varios sumandos iguales, (la potenciación se considera una multiplicación abreviada).
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente,
que se escribe en forma de superíndice. El exponente determina la
cantidad de veces que la base se multiplica por sí misma. Por ejemplo:

en general:

Una de las definiciones de la potenciación, por recursión, es la siguiente:
x1 = x
Si en la segunda expresión se toma a=1, se tiene que x¹ = x·x0. Al dividir los dos términos de la igualdad por x (que se puede hacer siempre que x sea distinto de 0), queda que x0=1.
Así que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacio o simplemente por analogía con el resto de números.
Para convertir una base con exponente negativo a positivo se pone la
inversa de la base, es decir que la potencia pasa con exponente
positivo.
Normalmente, las potencias con base 10, por la cantidad que
represente el exponente,esa será la cantidad de ceros en el resultado.
El resto de la bases, para sacar el resultado el número se multiplica
por sí mismo cuantas veces indique el exponente.
Propiedades de la potenciación
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
 si se cumple que
si se cumple que 
00 es una indeterminación. Que puede relacionarse con la indeterminación dado que
dado que

Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
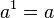
ejemplo:

Producto de potencias de igual base
El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes.

ejemplos:

División de potencias de igual base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos..
Se coloca la misma base y se restan los exponentes.

Potencia de un producto
la potencia de un producto de base (a·b) y de exponente "n" es igual
a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica
por el exponente.
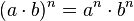
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a
elevada a la multiplicación de ambos exponentes. Se coloca la misma
base y se multiplican los exponentes. así se obtiene esta potencia
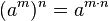
Producto de potencias de base distinta
En forma más general, la suma de dos radicaciones de base distinta a, b se puede expresar de la siguiente manera:

De tal forma que si a = b se regresa a la expresión para bases iguales.
Propiedad distributiva
a multiplicación y a
la división, pero no lo es con respecto a la suma ni a la resta.
Es distributiva con respecto a la multiplicación y división:
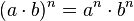

No es distributiva con respecto a la adición y sustracción:

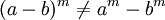
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación,
exceptuando aquellos casos en que base y exponente tienen el mismo
valor o son equivalentes.
En general:

Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.

Potencia de base 10
Toda potencia de base 10 y exponente natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
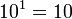

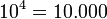

Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción no es irreductible, y en la que se cumple que
Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Potencia de números complejos
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente,
que se escribe en forma de superíndice. El exponente determina la
cantidad de veces que la base se multiplica por sí misma. Por ejemplo:

en general:

Una de las definiciones de la potenciación, por recursión, es la siguiente:
x1 = x

Si en la segunda expresión se toma a=1, se tiene que x¹ = x·x0. Al dividir los dos términos de la igualdad por x (que se puede hacer siempre que x sea distinto de 0), queda que x0=1.
Así que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacio o simplemente por analogía con el resto de números.
Para convertir una base con exponente negativo a positivo se pone la
inversa de la base, es decir que la potencia pasa con exponente
positivo.
Normalmente, las potencias con base 10, por la cantidad que
represente el exponente,esa será la cantidad de ceros en el resultado.
El resto de la bases, para sacar el resultado el número se multiplica
por sí mismo cuantas veces indique el exponente.
Propiedades de la potenciación
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
 si se cumple que
si se cumple que 
00 es una indeterminación. Que puede relacionarse con la indeterminación
 dado que
dado que
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
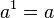
ejemplo:

Producto de potencias de igual base
El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes.

ejemplos:

División de potencias de igual base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos..
Se coloca la misma base y se restan los exponentes.

Potencia de un producto
la potencia de un producto de base (a·b) y de exponente "n" es igual
a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica
por el exponente.
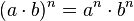
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a
elevada a la multiplicación de ambos exponentes. Se coloca la misma
base y se multiplican los exponentes. así se obtiene esta potencia
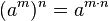
Producto de potencias de base distinta
En forma más general, la suma de dos radicaciones de base distinta a, b se puede expresar de la siguiente manera:

De tal forma que si a = b se regresa a la expresión para bases iguales.
Propiedad distributiva
a multiplicación y a
la división, pero no lo es con respecto a la suma ni a la resta.
Es distributiva con respecto a la multiplicación y división:
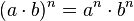

No es distributiva con respecto a la adición y sustracción:

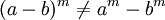
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación,
exceptuando aquellos casos en que base y exponente tienen el mismo
valor o son equivalentes.
En general:

Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.

Potencia de base 10
Toda potencia de base 10 y exponente natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
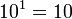

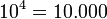

Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción no es irreductible, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Potencia de números complejos
Para cualquiera de los numeros reales  se tiene la identidad:
se tiene la identidad:
 se tiene la identidad:
se tiene la identidad:
Leonhard Euler
(Basilea, Suiza, 1707-San Petersburgo, 1783) Matemático suizo. Las facultades que desde temprana edad demostró para las matemáticas pronto le ganaron la estima del patriarca de los Bernoulli, Johann, uno de los más eminentes matemáticos de su tiempo y profesor de Euler en la Universidad de Basilea. Tras graduarse en dicha institución en 1723, cuatro años más tarde fue invitado personalmente por Catalina I para convertirse en asociado de la Academia de Ciencias de San Petersburgo, donde coincidió con otro miembro de la familia Bernoulli, Daniel, a quien en 1733 relevó en la cátedra de matemáticas.

Leonhard Euler
A causa de su extrema dedicación al trabajo, dos años más tarde perdió la visión del ojo derecho, hecho que no afectó ni a la calidad ni al número de sus hallazgos. Hasta 1741, año en que por invitación de Federico el Grande se trasladó a la Academia de Berlín, refinó los métodos y las formas del cálculo integral (no sólo gracias a resultados novedosos, sino también a un cambio en los habituales métodos de demostración geométricos, que sustituyó por métodos algebraicos), que convirtió en una herramienta de fácil aplicación a problemas de física. Con ello configuró en buena parte las matemáticas aplicadas de la centuria siguiente (a las que contribuiría luego con otros resultados destacados en el campo de la teoría de las ecuaciones diferenciales lineales), además de desarrollar la teoría de las funciones trigonométricas y logarítmicas (introduciendo de paso la notación e para definir la base de los logaritmos naturales).
En 1748 publicó la obra Introductio in analysim infinitorum, en la que expuso el concepto de función en el marco del análisis matemático, campo en el que así mismo contribuyó de forma decisiva con resultados como el teorema sobre las funciones homogéneas y la teoría de la convergencia. En el ámbito de la geometría desarrolló conceptos básicos como los del ortocentro, el circuncentro y el baricentro de un triángulo, y revolucionó el tratamiento de las funciones trigonométricas al adoptar ratios numéricos y relacionarlos con los números complejos mediante la denominada identidad de Euler; a él se debe la moderna tendencia a representar cuestiones matemáticas y físicas en términos aritméticos.
En el terreno del álgebra obtuvo así mismo resultados destacados, como el de la reducción de una ecuación cúbica a una bicuadrada y el de la determinación de la constante que lleva su nombre. A lo largo de sus innumerables obras, tratados y publicaciones introdujo gran número de nuevas técnicas y contribuyó sustancialmente a la moderna notación matemática de conceptos como función, suma de los divisores de un número y expresión del número imaginario raíz de menos uno. También se ocupó de la teoría de números, campo en el cual su mayor aportación fue la ley de la reciprocidad cuadrática, enunciada en 1783.
A raíz de ciertas tensiones con su patrón Federico el Grande, regresó nuevamente a Rusia en 1766, donde al poco de llegar perdió la visión del otro ojo. A pesar de ello, su memoria privilegiada y su prodigiosa capacidad para el tratamiento computacional de los problemas le permitieron continuar su actividad científica; así, entre 1768 y 1772 escribió sus Lettres à une princesse d’Allemagne, en las que expuso concisa y claramente los principios básicos de la mecánica, la óptica, la acústica y la astrofísica de su tiempo.
De sus trabajos sobre mecánica destacan, entre los dedicados a la mecánica de fluidos, la formulación de las ecuaciones que rigen su movimiento y su estudio sobre la presión de una corriente líquida, y, en relación a la mecánica celeste, el desarrollo de una solución parcial al problema de los tres cuerpos –resultado de su interés por perfeccionar la teoría del movimiento lunar–, así como la determinación precisa del centro de las órbitas elípticas planetarias, que identificó con el centro de la masa solar. Tras su muerte, se inició un ambicioso proyecto para publicar la totalidad de su obra científica, compuesta por más de ochocientos tratados, lo cual lo convierte en el matemático más prolífico de la historia.
Suscribirse a:
Comentarios (Atom)








